중등 1학년 수학 > 입체도형의 겉넓이와 부피 > 구의 부피, 구의 겉넓이 공식 쉽게 암기하는 법, 연습문제 프린트 학습지

구의 부피
$$V=\dfrac{4}{3}\pi r^3$$
구의 겉넓이
$$S=4\pi r^2$$
구의 부피 공식과 겉넓이 공식은 많은 학생들이 암기하고 있지만 시간이 흐르면서 조금씩 헷갈리거나 잊어버리는 경우가 많은데요,
공식을 조금이라도 오래 기억하기 위해서는 공식의 모양과 생김새를 어떤 식으로든 연결시키거나 연상하는 방법으로 익히면 도움이 될거에요.
특히, 구의 겉넓이 공식과 구의 부피 공식은 공통 인수가 $4\pi r$로서 거의 대부분의 식을 공유하고 있어요.
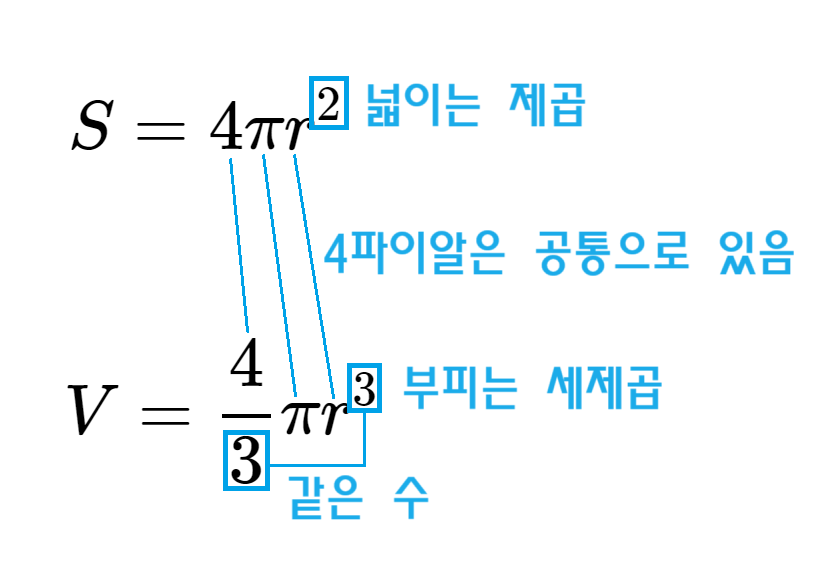
이렇게 공식을 암기해보았어요.
구와 관련된 문제를 몇개 풀어보도록 하겠습니다.

반지름이 $7cm$인 구의 겉넓이는 $S=4\times{\pi}\times{7^2}=196\pi cm^2$이고 구의 부피는 $V=\dfrac{4}{3}\times{\pi}\times{7^3}=\dfrac{1372}{3}\pi cm^3$

이 구는 전체를 1이라고 할 때 $\dfrac{3}{4}$의 비율로 구성된 구라고 할 수 있어요. 겉넓이를 구해보겠습니다.
반지름이 $2 cm$이므로 구의 겉넓이는 $S= (4\times{\pi}\times{2^2})\times{\dfrac{3}{4}}+(\pi\times{2^2})=16\pi cm^2$
이렇게 구의 부피와 공식을 공부하고 연습문제 풀이를 해보았습니다.
수학에 자신감은 문제를 직접 손으로 풀 때 향상 되는데요, 수학 문제를 더 많이 연습하고 싶으시면 '모두매쓰'에서 문제를 만들어 풀어보시길 추천드립니다.
아래는 모두매쓰에서 만든 문제 이미지인데요, 클릭하시면 모두매쓰 사이트로 이동합니다.
그럼 좋은 하루 되세요~
중등 1학년 수학 > 입체도형의 겉넓이와 부피 > 구의 부피, 구의 겉넓이 공식 쉽게 암기하는 법, 연습문제 프린트 학습지
'중등수학' 카테고리의 다른 글
| 중등 3학년 수학 > 삼각비 > 보조선을 긋는 삼각형의 넓이 구하는 연습문제 프린트 학습지 (0) | 2024.07.07 |
|---|---|
| 중등 1학년 수학 > 평행선의 성질 > 보조선을 긋는 평행선의 성질 연습문제 프린트 학습 (0) | 2024.07.07 |
| 중등 1학년 수학 > 원과 부채꼴 > 부채꼴의 넓이, 부채꼴의 호의 길이 공식과 원리, 연습문제 프린트 학습지 (0) | 2024.07.07 |
| 중등 3학년 수학 > 이차함수 > 이차함수의 그래프를 보고 함수식을 구하기 연습문제 프린트 학습지 (0) | 2024.07.06 |
| 중등 2학년 수학 > 이등변삼각형 > 이등변삼각형의 성질 증명 개념 연습문제 프린트 학습지 (0) | 2024.07.06 |





