고등 수학(상) > 인수분해 > 고차식의 인수분해 연습문제 프린트 학습지
차수가 보통 3차 이상의 식을 고차식이라고 부르고, 이를 인수분해하는 문제를 고차식의 인수분해라고 합니다.
그럼 인수분해란 무엇일까요?
인수분해란 어떤 식을 두 개 이상의 식의 곱으로만 나타내는 것을 말해요.
가령, $ma+mb$라는 식을 $m\times{(a+b)}=m(a+b)$로 나타내는 것을 인수분해한다고 합니다.
인수분해가 왜 중요할까요?
역시 방정식과 관련이 있습니다.
예를 들어, $x^2-x-2=0$이라는 이차방정식이 있다고 하면,
$(x+1)(x-2)=0$으로 인수분해를 할 수 있고, 이를 통해 방정식의 해가 $x=1$ 또는 $x=-2$라는 것을 아주 쉽게 알 수 있습니다.
다시 말해,
$x^2-x-2=0$과 $(x+1)(x-2)=0$은 단지 인수분해를 했고 안했고의 문제일 뿐이지만,
해가 바로 보이지 않던 것이 바로 보이는 놀라운 효과를 가져옵니다.
식의 변화가 문제를 해결하는 것입니다. 이외에도 식을 인수분해하는 것은 복잡한 식을 작은 단위의 식의 곱으로 묶어서 하나씩 해결한다는 의미를 지닌다고 생각합니다.
그럼, 고차식의 인수분해 문제를 풀어보겠습니다.
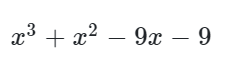
만약 $f(x)=x^3+x^2-9x-9$라고 한다면,
$f(a)=0$을 만족하는 $x=a$의 값을 찾아야 합니다.
위 식에서 $x=-1$이라고 하면,
$f(-1)=(-1)^3+(-1)^2-9\times{(-1)}-9=0$
을 만족하므로 $x=-1$을 찾은 것입니다.
이걸 어떻게 활용할까요?
인수정리라는 개념이 있는데요,
인수정리란 다항식 $f(x)$를 일차식 $(x-a)$로 나누었을 때 나머지가 $0$이면 다음과 같이 식을 나타낼 수 있다는 개념입니다.
$f(x)=(x-a)Q(x)$
이때 (x-a)를 인수라고 부르고, $(x-a)Q(x)$는 인수분해된 식이라고 부릅니다.
위 식에 $x=a$를 대입하면 어떻게 될까요?
$f(a)=0$이 됩니다.
그러니까 $f(a)=0$이라는 것은 $f(x)=(x-a)Q(x)$식을 전제하므로, 다항식을 거꾸로 추론하는 개념입니다.
그럼 위 식에서 $x=-1$일 때 $f(-1)=0$이므로 이런 형태의 식으로 인수분해가 됨을 알 수 있어요.
$f(x)=(x+1)Q(x)$
그럼 다시 $Q(x)$가 어떤 식인지만 알면 인수분해는 완성이 되는 것입니다.
$Q(x)$는 어떻게 구할까요?
조립제법
조립제법이란 다항식 $f(x)$를 일차식으로 나눌 때, 각 항들의 계수들만 따로 뽑아서 간편하게 다항식의 나눗셈을 하는 방법입니다.

몫이 $x^2-9$이므로
$f(x)=x^3+x^2-9x-9=(x+1)(x^2-9)$
$=(x+1)(x+3)(x-3)$
으로 인수분해가 마무리 되었습니다.
[고차식의 인수분해 연습문제: 모두매쓰에서 생성]
고등 수학(상) > 인수분해 > 고차식의 인수분해 연습문제 프린트 학습지
'고등수학' 카테고리의 다른 글
| 고등 수학(상) > 항등식과 나머지정리 > 완전제곱꼴인 이차식으로 나누었을 때의 나머지 구하기 연습문제 프린트 학습지 (0) | 2024.07.29 |
|---|---|
| 고등 수학(상) > 항등식과 나머지정리 > 다항식 P(x)를 일차식으로 나눈 나머지 구하기 연습문제 프린트 학습지 (0) | 2024.07.29 |
| 고등 수학(상) > 인수분해 > 복이차식의 인수분해 연습문제 프린트 학습지 (0) | 2024.07.29 |
| 고등 수학II > 도함수의 활용 > 방정식이 세 실근을 가지 위한 k의 값의 범위 구하기 연습문제 프린트 학습지 (0) | 2024.07.29 |
| 고등 수학II > 도함수의 활용 > 닫힌 구간에서 부등식이 항상 성립하도록 하는 실수 a의 값이 범위 구하기 연습문제 프린트 학습지 (0) | 2024.07.29 |





