고등 수학II > 도함수의 활용 > 방정식이 세 실근을 가지 위한 k의 값의 범위 구하기 연습문제 프린트 학습지
안녕하세요. 오늘은 도함수의 활용 중 방정식의 실근의 개수를 구하는 문제를 풀어보겠습니다.
방정식의 실근이라는 테마는 수학에서 특히 함수 단원에서 무척 중요하게 다루어지는데요,
왜냐하면 방정식의 실근이 존재하는지 유무와 그 값의 위치는 수학의 연구 과제를 해결는데에 함수의 그래프 등 기하학의 도움을 많이 받기 때문인데요.
방정식의 실근은 함수의 그래프와 일맥상통하는 부분이 있습니다. 만약 어떤 수학 문제에서 '실근'이라는 단어가 등장한다면 반드시 '그래프'를 떠올리고 문제를 해결하길 바랍니다.
그럼 문제를 풀어보도록 할게요.

좌변에 포함된 $k$를 우변으로 이항하면,
$x^3-12x+5=-k$
와 같은 식이 만들어지는데요,
방정식이 서로 다른 세 실근을 가진다는게 무슨 의미인지 우선 나중에 생각해보기로 하고,
그래프적인 사고를 먼저 해볼게요.
좌변의 식을 함수로 해석하면, $y=x^3-12x+5$인 삼차함수이고, 우변의 식을 함수로 해석하면 $y=-k$인 상수함수입니다.
각각의 그래프를 그려보도록 할게요.
$y=f(x)=x^3-12x+5$를 미분하면,
$y'=f'(x)=3x^2-12$인데요,
$f'(x)=0$을 만족하는 $x$의 값을 찾으면 어느 구간에서 극점을 가지는지 알 수 있어요.
$f'(x)=3x^2-12=0$
$3(x^2-4)=0$
$3(x+2)(x-2)=0$
$x=2$ 또는 $x=-2$
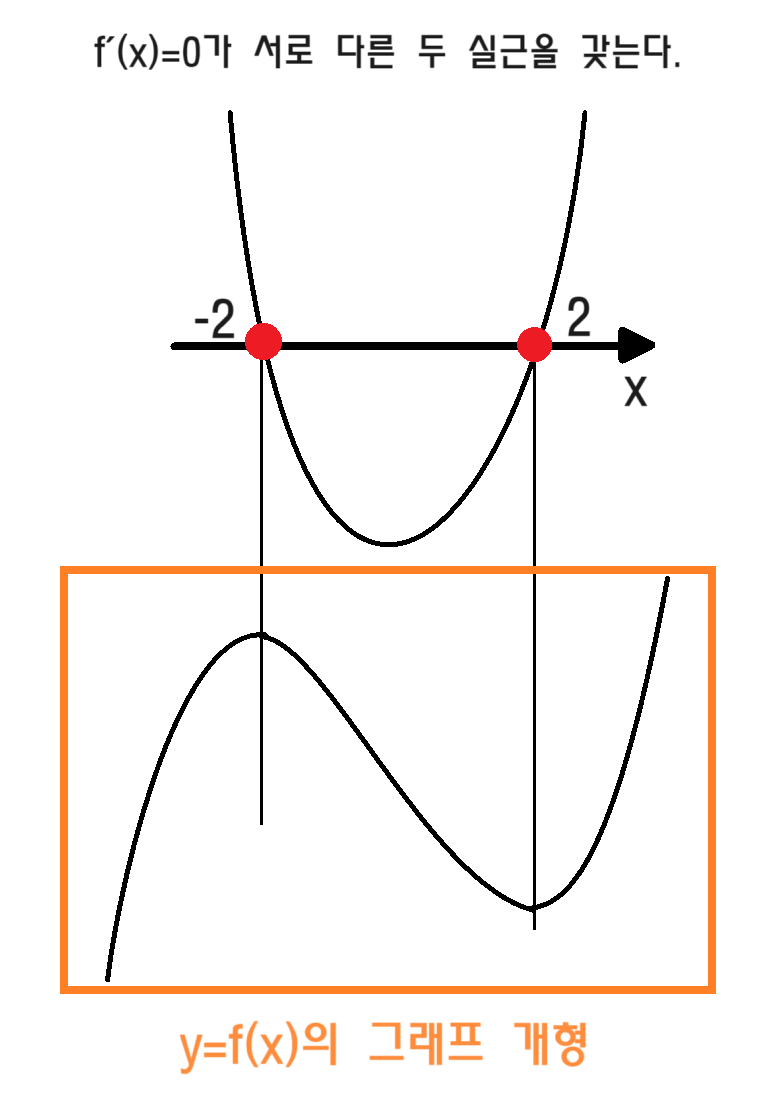
삼차함수의 개형이 나왔어요.
$x=-2$일 때, 극대이고, $x=2$일 때 극소를 가지네요. 극값을 구하고 그래프를 그려보겠습니다.
$y=f(x)=x^3-12x+5$ 이므로
$f(-2)=(-2)^3-12\times{(-2)}+5=-8+24+5=21$
$f(2)=2^3-12\times{2}+5=8-24+5=-11$

좌변의 함수식 $y=x^3-12x+5$의 그래프를 그렸으니 이제 우변의 함수식 $y=-k$의 그래프를 그려보면,

서로 다른 3개의 교점이 생기도록 선을 그었는데요, 바로 저렇게 되었을 때, 방정식 $x^3-12x+5=-k$는 서로 다른 세 실근을 가집니다. 즉 우변의 $-k$를 원래대로 좌변으로 이동시켜도 $x^3-12x+5+k=0$이며 방정식의 해는 동일하게 서로 다른 세 실근을 가집니다.
문제에서는 $k$의 값의 범위를 묻고 있는데요, 즉 $k$의 값이 하나가 아니라는 얘기예요.
그래프를 다시 보면, $y=-k$의 그래프가 상하로 이동할 때 서로 다른 3개의 교점을 가지는 범위를 생각할 수 있어요.

그렇다면, 만약 $y=-k$의 그래프가 극점을 지나게 되면 어떨까요?
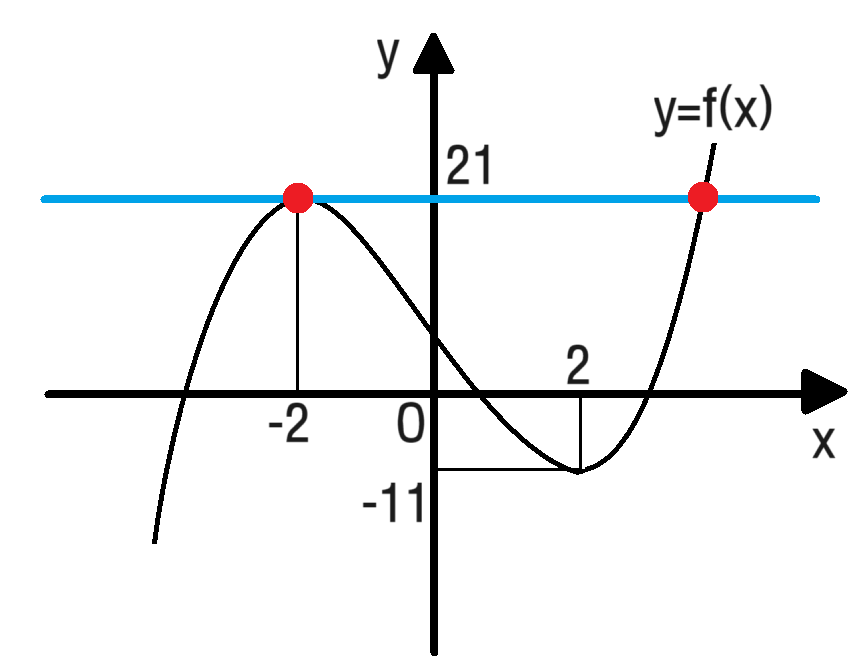
이 경우에는 교점이 2개인데요, 하나는 접점이고 다른 하나는 그냥 지나는 점이에요.
이때 방정식의 실근은 하나는 중근, 다른 하나는 중근이 아닌 실근이 나옵니다. 서로 다른 두 개의 실근이 나온다고 할 수 있어요. 이렇게 교점의 개수와 종류에 따라서 방정식의 실근의 개수와 종류도 함께 대응되는 관계가 있다는 걸 알 수 있죠.
결국, $y=-k$는 극점을 지나면 안되고 그 사이에 위치해야해요.
$21>-k>-11$
$-21<k<11$
이렇게 문제를 풀어보았습니다. 이 문제에서 물어보는 사항은 다음과 같아요.
1. 방정식의 실근을 그래프로 해석하는 관계를 알고 있는가.
2. 삼차함수의 그래프를 그릴 수 있는가.
3. 서로 다른 세 실근이 가질 때, 교점이 3개가 되도록 두 그래프를 활용할 수 있는가.
이 문제는 특히 모의고사나 수능에서 4점 이상으로 나오는 대부분의 문제에서 빠지지 않고 등장하는 개념이기 때문에 충분히 연습하기를 바랍니다. 연습만 한다면 어렵지 않습니다.
아래는 수학 문제를 생성하여 프린트 할 수 있는 모두매쓰에서 만든 연습문제입니다.
연습문제를 활용하셔서 마스터하시기 바래요.
그럼 오늘도 좋은 하루되세요.
[모두매쓰 생성 연습문제]
고등 수학II > 도함수의 활용 > 방정식이 세 실근을 가지 위한 k의 값의 범위 구하기 연습문제 프린트 학습지
'고등수학' 카테고리의 다른 글
| 고등 수학(상) > 인수분해 > 고차식의 인수분해 연습문제 프린트 학습지 (0) | 2024.07.29 |
|---|---|
| 고등 수학(상) > 인수분해 > 복이차식의 인수분해 연습문제 프린트 학습지 (0) | 2024.07.29 |
| 고등 수학II > 도함수의 활용 > 닫힌 구간에서 부등식이 항상 성립하도록 하는 실수 a의 값이 범위 구하기 연습문제 프린트 학습지 (0) | 2024.07.29 |
| 고등 수학I > 수열의 합 > 자연수의 거듭제곱의 합 공식, 연습문제 프린트 학습지 (0) | 2024.07.20 |
| 고등 수학I > 삼각함수 > 각변환공식, 일반각에 대한 삼각함수의 값의 계산 연습문제 프린트 학습지 (0) | 2024.07.20 |





