고등 수학II > 도함수의 활용 > 닫힌 구간에서 부등식이 항상 성립하도록 하는 실수 a의 값이 범위 구하기 연습문제 프린트 학습지

고등 수학II > 도함수의 활용 > 닫힌 구간에서 부등식이 항상 성립하도록 하는 실수 a의 값이 범위 구하기 연습문제 프린트 학습지

안녕하세요. 오늘은 도함수의 활용 문제 유형 중 부등식이 항상 성립하는 조건을 해결하는 문제 유형을 다루겠습니다.

사실 이 유형은 함수의 최댓값과 최솟값의 유형이라고 보아도 무방한데요,

거듭 강조하지만, 도함수의 활용 문제의 시작과 끝은 '함수의 그래프'입니다. 함수의 그래프를 쉽게 그릴 수 있으면 그에 비례해서 다양한 유형의 도함수의 활용 문제가 해결이 됩니다.

이와 관련해서 참고할만한 글이 있으니 함수의 그래프 개형에 대해 정리가 되어 있지 않다면 아래 글을 먼저 보시기를 추천드립니다.

삼차함수의 최댓값과 최솟값

그럼 문제를 풀어보도록 하겠습니다.

좌변은 삼차함수, 우변은 상수함수으로 만들고, 상수함수의 높낮이를 항상 만족하는 문제로 생각할 수 있습니다.

$x^3+3x^2-24x-5≥-a$

우선 좌변을 $y=x^3+3x^2-24x$로 해석하여 그래프를 나타내보겠습니다.

미분을 하면,

$y'=3x^2+6x-24$

인데요, 그래프의 개형을 알아보기 위해 $f'(x)=0$꼴의 방정식을 만듭니다.

$3x^2+6x-24=0$

$3(x^2+2x-8)=0$

$3(x+4)(x-2)=0$

따라서 $x=-4$ 또는 $x=2$에서 기울기가 $0$이 됩니다.

삼차함수의 개형을 찾았으니 극값을 구하고 좌표평면 위에 적절한 위치로 나타냅니다.

극댓값과 극솟값을 구하기 전에 먼저 정의역구간을 살펴보면, $[-1,2]$이므로

구간 밖에 극값이 있으면 굳이 필요하지 않은 계산을 하지 않아도 됩니다.

참고로 최댓값과 최솟값을 찾는 방법은,

1. 닫힌 구간의 양끝 함수값을 구한다.

2. 닫힌 구간 내에서의 극값을 구한다.

3. 그 중에서 최댓값과 최솟값을 찾는다.

$y=f(x)=x^3+3x^2-24x$ 에서

$f(-1)=(-1)^3+3\times{(-1)}^2-24\times{(-1)}=-1+3+24=26$

$f(2)=2^3+3\times{2}^2-24\times{2}=8+12-48=-28$

이 값을 바탕으로 좌표평면 위에 그래프를 나타내면, 다음과 같습니다.

이제 문제의 90%는 푼 셈인데요, 다시 문제를 가져와볼게요.

좌변의 $a$를 우변으로 이항하여,

$x^3+3x^2-24x-5≥-a$

부등식의 좌변을 $y=x^3+3x^2-24x-5$인 함수로 해석하여 그래프를 그린게 위 그래프입니다. 이때 정의역 구간이 $[-1,2]$이므로 빨간색 라인으로 구간안에서의 최댓값과 최솟값을 구한 상태예요.

그럼 위 부등식이 항상 성립하기 위해서는

이런 과정이 필요해요.

따라서 그래프에서 최솟값이 되는 점을 만나거나 아랫부분에 $y=-a$가 그려져야해요.

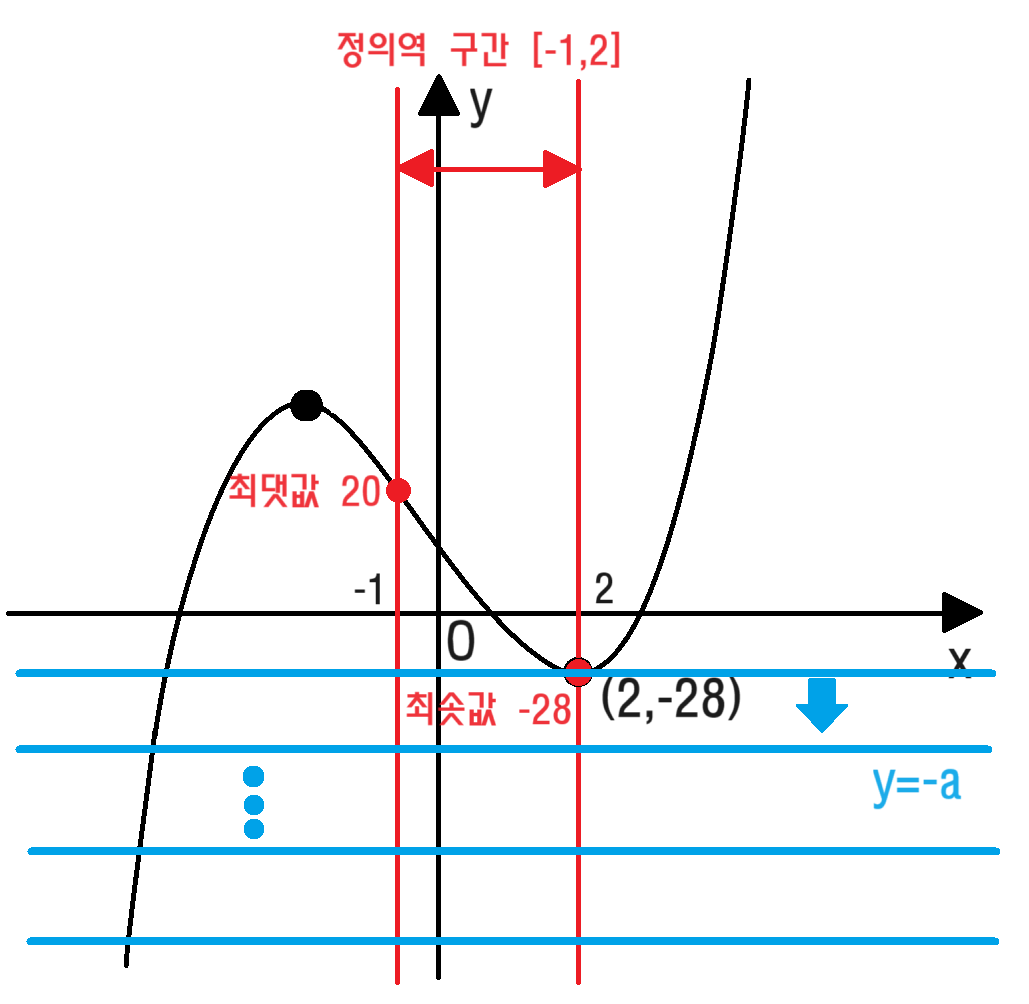
따라서 $y=-a$의 상수함수에서 $-a$의 값이 최솟값에 해당하는 $-28$보다 작거나 같아야 부드식이 항상 성립합니다.

$-a≤-28$

$a≥28$

이렇게 $a$의 값을 구하였는데요,

이 문제는 이 문제는 다음을 체크하는 문제예요.

1. 삼차함수의 그래프를 잘 그릴 수 있는가.

2. 정의역 구간이 주어질 때, 최댓값과 최솟값을 구할 수 있는가.

3. 부등식이 항상 성립하는 조건을 그래프로 해석할 수 있는가.

입니다. 이 문제만 연습을 많이 하셔도 도함수의 활용 단원을 마스터하실 수 있을거에요.

이 문제와 같은 유형의 문제를 무제한으로 생성하여 프린트 할 수 있는 '모두매쓰' 사이트를 이용하시기를 바랍니다.

그럼 오늘도 즐거운 하루되세요.

[모두매쓰 생성 연습문제]