고등 수학(상) > 이차부등식 > 두 함수 y=f(x), y=g(x)의 그래프로 이차부등식의 해 구하기 연습문제 프린트 학습지
이차함수의 그래프를 보고 이차부등식의 해를 구하는 문제를 풀어보도록 하겠습니다.
이차함수의 그래프와 이차부등식의 관계를 먼저 설명을 간단히 할게요.
만약 두 함수 $f(x)$, $g(x)$가 있다고 하겠습니다.
$f(x)$는 이차함수, $g(x)$는 일차함수라고 할 때,

이것은 부등식의 해를 찾는 원리에 중요한 단서를 제공합니다. 거꾸로 생각하면 부등식 문제와 방정식 문제가 되기 때문입니다.
$y=f(x)$의 그래프를 기준으로 이야기를 해보면,
$x=2$일 때, $y=f(x)$의 그래프가 $y=g(x)$의 그래프보다 위에 있다고 할 수 있습니다.
$x=5$일 때, $y=f(x)$의 그래프가 $y=g(x)$의 그래프보다 아래에 있다고 할 수 있습니다.
$x=7$일 때, $y=f(x)$의 그래프가 $y=g(x)$의 그래프가 만난다(또는 교점을 가진다)고 할 수 있습니다.
이것을 아래와 같이 표현할 수도 있어요.
$x=2$일 때, $y=f(x)$의 함수값이 $y=g(x)$의 함수값보다 크다고 할 수 있습니다.($f(2)>g(2)$)
$x=5$일 때, $y=f(x)$의 함수값이 $y=g(x)$의 함수값보다 작다고 할 수 있습니다.($f(5)<g(5)$)
$x=7$일 때, $y=f(x)$의 함수값이 $y=g(x)$의 함수값과 같다고 할 수 있습니다.($f(7)=g(7)$)
그럼 한 번 질문을 해볼게요.
1. $y=f(x)$의 그래프가 $y=g(x)$의 그래프보다 위에 있는 $x$의 값은 $2$ 이외에 또 있을까요? 있다면 어디에 있을까요?
2. $y=f(x)$의 그래프가 $y=g(x)$의 그래프보다 아래에 있는 $x$의 값은 $5$ 이외에 또 있을까요? 있다면 어디에 있을까요?
3. $y=f(x)$의 그래프가 $y=g(x)$의 그래프와 만날 때 $x$의 값은 $7$ 이외에 또 있을까요? 있다면 어디에 있을까요?
여기에 대한 답을 하는 것이 바로 부등식의 해와 방정식의 해입니다.
1번 질문에 답을 해보겠습니다.
$y=f(x)$의 그래프가 $y=g(x)$의 그래프보다 위에 있는 $x$의 값은 $2$ 이외에 또 있을까요? 있다면 어디에 있을까요?
이 문제를 해결하기 위해서는 부등식 $f(x)>g(x)$, 즉 $f(x)$의 함수값이 $g(x)$의 함수값보다 커야 그래프로 나타낼 때 위에 있습니다.
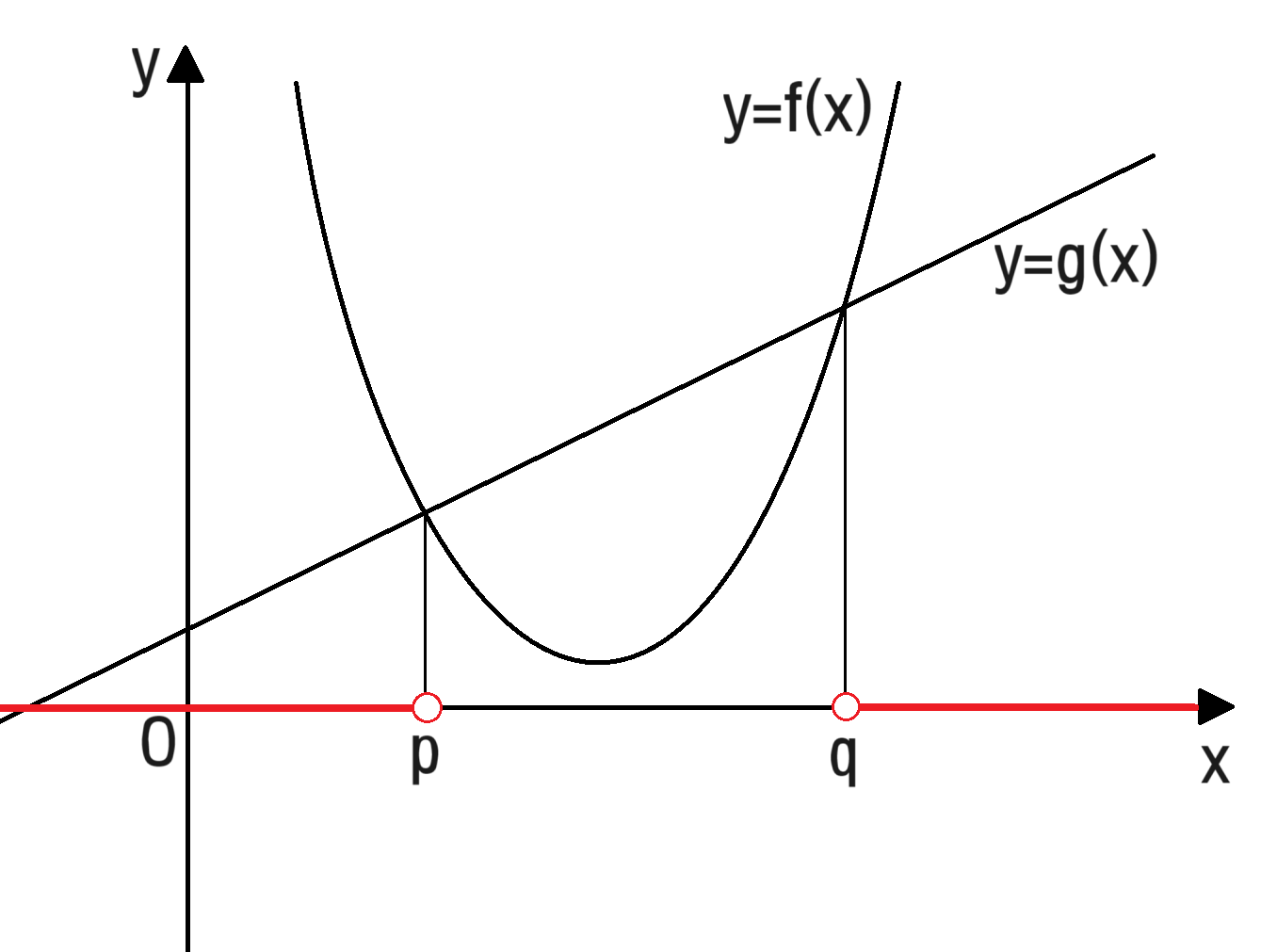
이 질문에 대한 답은 위와 같습니다. $x<p$ 또는 $x>q$일 때 $y=f(x)$의 그래프가 $y=g(x)$의 그래프보다 위에 있습니다.
다음 질문은,
$y=f(x)$의 그래프가 $y=g(x)$의 그래프보다 아래에 있는 $x$의 값은 $5$ 이외에 또 있을까요? 있다면 어디에 있을까요?
이 질문에 답을 하려면 부등식 $f(x)<g(x)$, 즉 $f(x)$의 함수값이 $g(x)$의 함수값보다 작아야 그래프로 나타낼 때 아래에 있습니다.

위 그림과 같이 $x$의 범위가 $p<x<q$일 때, $y=f(x)$의 그래프가 $y=g(x)$의 그래프보다 아래에 있습니다. $x=5$ 이외에도 무수히 많은 $x$의 값이 있습니다.
마지막 질문은,
$y=f(x)$의 그래프가 $y=g(x)$의 그래프와 만날 때 $x$의 값은 $7$ 이외에 또 있을까요? 있다면 어디에 있을까요?
두 함수의 그래프가 만난다는 것은 함수값이 같을 때입니다.

$x=p$일 때, $f(p)$의 값과 $g(p)$의 값이 같고, $x=q$일 때, $f(q)$의 값과 $g(q)$의 값이 같습니다.
따라서 2개의 교점을 가집니다.
이차함수와 부등식, 이차함수와 방정식의 관계를 정리하면 다음과 같습니다.
두 함수 $y=f(x)$와 $y=g(x)$에서
1. $y=f(x)$의 그래프가 $y=g(x)$의 그래프보다 위쪽에 있는 $x$의 범위를 찾기 위해서는
$f(x)>g(x)$를 만족하는 해를 구한다.
2. $y=f(x)$의 그래프가 $y=g(x)$의 그래프보다 아래쪽에 있는 $x$의 범위를 찾기 위해서는
$f(x)<g(x)$를 만족하는 해를 구한다.
3. $y=f(x)$의 그래프가 $y=g(x)$의 그래프와 교점을 가지는(=만나는) $x$의 범위를 찾기 위해서는
$f(x)=g(x)$를 만족하는 해를 구한다.
반대로 말할 수도 있습니다.
1. $f(x)>g(x)$를 만족하는 해를 구하면, 그 해에서 $y=f(x)$의 그래프가 $y=g(x)$의 그래프보다 위쪽에 있다.
2. $f(x)<g(x)$를 만족하는 해를 구하면, 그 해에서 $y=f(x)$의 그래프가 $y=g(x)$의 그래프보다 아래쪽에 있다.
3. $f(x)=g(x)$를 만족하는 해를 구하면, 그 해에서 $y=f(x)$의 그래프가 $y=g(x)$는 교점을 가진다(=만난다).
함수와 부등식, 함수와 방정식이 어떻게 관계를 가지는지 정리해보았습니다.
이 개념은 너무나도 중요하고, 또 고등학교 수학 전체에서 어쩌면 가장 중요한 위치를 지니는 부분이라고 할 수 있습니다.
차근차근 학습하기 바랍니다.
아래는 부등식의 해를 연습할 수 있는 연습문제입니다.
<모두매쓰 생성 연습문제>
고등 수학(상) > 이차부등식 > 두 함수 y=f(x), y=g(x)의 그래프로 이차부등식의 해 구하기 연습문제 프린트 학습지
'고등수학' 카테고리의 다른 글
| 고등 수학I > 수열의 합 > 자연수의 거듭제곱의 합 공식, 연습문제 프린트 학습지 (0) | 2024.07.20 |
|---|---|
| 고등 수학I > 삼각함수 > 각변환공식, 일반각에 대한 삼각함수의 값의 계산 연습문제 프린트 학습지 (0) | 2024.07.20 |
| 고등 수학I > 수열 > 등차수열의 합 공식과 계산 연습문제 프린트 학습지 (0) | 2024.07.19 |
| 고등 수학I > 삼각함수의 그래프 > 절댓값 기호가 포함된 함수의 그래프 연습문제 프린트 학습지 (0) | 2024.07.18 |
| 고등 수학I > 삼각함수의 그래프 > 함수의 그래프를 보고 미지수 구하기 연습문제 프린트 학습지 (0) | 2024.07.18 |




