중등 2학년 수학 > 도형의 닮음 > 삼각형의 닮음 조건 개념, 연습문제 프린트 학습지

중등 2학년 수학 > 도형의 닮음 > 삼각형의 닮음 조건 개념, 연습문제 프린트 학습지

 

닮음

 

닮음이란 도형의 크기를 확대 또는 축소할 때, 두 도형이 겹치게 만들 수 있으면 두 도형은 닮았다고 합니다. 

닮음과 비슷한 개념으로 '합동'이 있어요. 합동은 확대 또는 축소가 아닌 상태에서 그대로 겹쳐지는 두 도형을 말합니다. 합동과 닮음은 조건이 비슷하기 때문에 잘 구별해서 공부해야 합니다. 

 

그럼, 삼각형에서 닮음의 조건이 무엇이 있는지 알아볼게요. 닮음의 종류는 총 3가지가 있어요. 

 

1.  AA닮음

 

보통 A는 Angle(각)의 줄임말이예요. AA는 두 각의 크기가 같은 조건을 뜻해요. 두 각의 크기가 같으면 왜 닮음일까요?

 

 

왜 AAA달음이 아닌 AA닮음일까요? 그 이유는 어차피 삼각형에서 두 각의 크기가 같으면 나머지 각의 크기는 자동으로 같을 수 밖에 없기 때문이랍니다. 따라서 두 각이 같으면 닮음이 됩니다. 

 

2.  SAS닮음

삼각형의 합동 조건과 굉장히 비슷하죠? SAS합동 조건과 다른 점은 S(변의 길이)가 똑같은게 아닌 비율로서 같음을 만족해야 하는거에요

. 두 변의 길이의 비율이 같고, 그 끼인각의 크기가 같으면 두 도형은 SAS닮음입니다. 위 그림과 같이 6 : 15와 2 : 5는 비율이 같아요. 그리고 끼인각의 크기가 같아요. 주의할 점은 끼인각이 같아야 한다는 점입니다. 그렇지 않은 각의 크기가 같으면 닮음이 아닙니다. 

 

3.  SSS닮음

세 변의 길이가 모두 같은 SSS합동 조건과 비슷하죠? 하지만 이것도 마찬가지로 완전히 같은 변의 크기가 아닌 비율이 같은 변이 3개가 모여야 SSS닮음이라고 할 수 있어요. 

이렇게 삼각형의 닮음 조건에 대해 알아봤어요. 특히 합동조건과 매우 유사한 부분이 있지만 중요한 것은 닮음의 S는 변의 길이가 아닌 변의 길이의 비율이라는 점을 다시 한 번 상기하며 공부하길 바랍니다. 

 

그럼 이제 문제를 몇 개 풀어보도록 하겠습니다. 

여기에서 먼저 닮음 조건을 만족하는 삼각형ADE와 삼각형ABC가 어떤 닮음 조건을 만족하는지 말할 수 있어야해요. 여기서는 AA닮음 조건을 만족한답니다. 왜냐하면 선분DE와 선분BC는 평행하기 때문에 동위각의 크기가 같다는 성질을 이용한거에요. 

 

그럼 이번에는 닮음비를 찾아야해요. 이때 주의해야하는 점은 아래와 같아요. 

단순히 $9:3$이라고 닮음비를 말해서는 안된답니다. 왜 그럴까요? 그 이유는 삼각형ADE와 삼각형ABC가 닮음 삼각형인데, 삼각형ADE의 한 변 AD에 대응되는 삼각형ABC의 변이 DB가 아니기 때문이예요. 

빨간색 빗금으로 표시한 선분끼리 닮음 삼각형의 대응하는 변이예요. 따라서 삼각형ABC의 대응변은 선분AB인 $12cm$가 됩니다. 

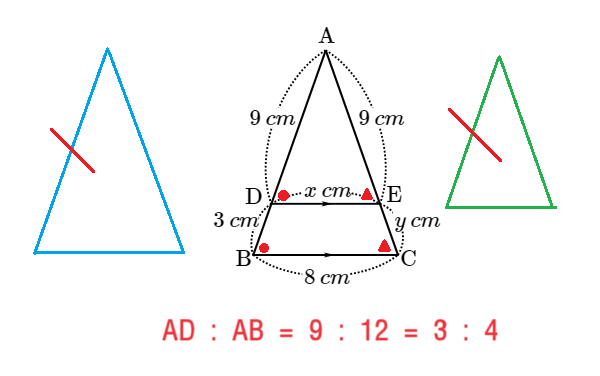
두 삼각형의 닮음비는 $3:4$이므로 $x$의 길이를 구하는 비례식은 다음과 같아요. 

$x:8=3:4$

$4x=24$

$x=6$

 

그리고 $y$의 길이도 구할 수 있는데요, $y$의 길이는 이등변삼각형이기 때문에 쉽게 $y=3$으로 구할 수 있어요. 

따라서 정답은 $x+y=6+3=9$가 됩니다. 

 

이렇게 삼각형의 닮음조건과 연습문제를 풀어보았습니다. 

추가로 더 많은 문제를 풀고 싶으시면 '모두매쓰'를 활용하시기를 추천드립니다. 

모두매쓰는 수학 문제를 만드는 사이트예요. 

그럼 좋은 하루 되세요~

중등 2학년 수학 > 도형의 닮음 > 삼각형의 닮음 조건 개념, 연습문제 프린트 학습지