중등 2학년 수학 > 일차함수 > 기울기 개념, 일차함수 연습문제 프린트 학습지
일차함수를 배울 때 가장 중요한 개념이 바로 '기울기'예요.
기울기란 '직선이 기울어진 정도를 나타내는 수'를 뜻하는데요, 그 이유는 일차함수의 그래프 모양 때문이에요.

'기울기'라는 용어는 사실상 우리가 일상생활에서 사용하는 언어를 가지고 와서 수학 개념을 쉽게 느끼도록 하기 위해 만든 용어인데요, 원래 정확한 명칭은 평균변화율이랍니다. 평균변화율과 기울기는 같은 개념이에요. 고등학교에서 배우는 '미분'에는 평균변화율과 순간변화율을 함께 공부해요.
저는 개인적으로 기울기라는 용어가 취지와 달리 오히려 수학을 더 헷갈리고 어렵게 만든다고 생각하는데요, 그 이유는 설명하는 과정에서 말씀드릴게요.
우선 기울기의 정의를 살펴보면 다음과 같아요.

몇 가지 예시를 보면서 기울기값이 어떻게 결정되는지 살펴볼게요.

직선 위의 2개의 점을 임의로 잡고 한 점이 다른 한 점으로 가는 방향에서 x값과 y값이 어떻게 변화하는지를 기울기로 나타내고 있어요.
기울기의 값이 양수이면 오른쪽 위를 향하고, 음수이면 오른쪽 아래로 향해요. 만약 기울기의 값이 '양수'만 있다면 우리가 생각하는 기울기라는 용어가 찰떡이겠지만, 기울기가 음수도 있기 때문에 용어에서 오는 혼란이 생겨요.
다음 그림을 살펴보면요,
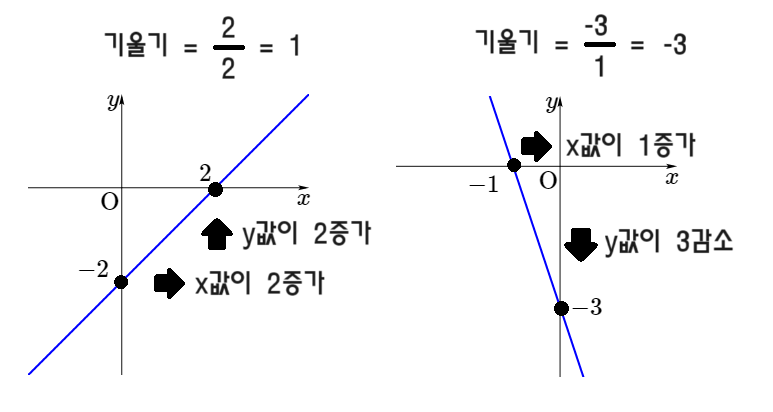
기울기를 용어 그대로 생각한다면 더 기울어진게 오른쪽 그림이지만, 실제로 그 값은 음수이기 때문에 왼쪽의 기울기가 더 큰 이상한 일이 발생하죠. 왜냐하면 왼쪽의 기울기는 '양수'이고, 오른쪽의 기울기는 '음수'이기 때문이에요. 그러므로 기울기라는 용어가 적합하지 않을수도 있다는게 개인적인 생각입니다.
굳이 기울기의 가파름의 정도로 말하려면 '절댓값'을 비교하는게 좋아요. 위 그림에서 오른쪽 그림의 직선의 기울기는 값은 음수라서 작지만, 절댓값은 |-3| = 3 으로 더 큽니다. 문제를 볼 때, 단순히 기울기값을 물어보는지, 기울기의 절댓값을 물어보는지 잘 살펴보는게 좋아요.
여기서 일차함수의 그래프를 그리는 문제를 풀어볼게요

이 문제의 y절편은 y축과 만나는 점인데요, y축 위의 점은 모두 x좌표가 0이므로 y=2x-1 에 x=0을 대입하면 y=-1, 즉 (0,-1)이 y축과 만나는점 다시말해 y절편이 됩니다.

y=2x-1 에서 x의 계수가 기울기이므로 2이고, 따라서 x가 2증가하면 y는 4만큼 증가한다는 걸 알 수 있어요.
문제를 하나 더 풀어보도록 할게요.
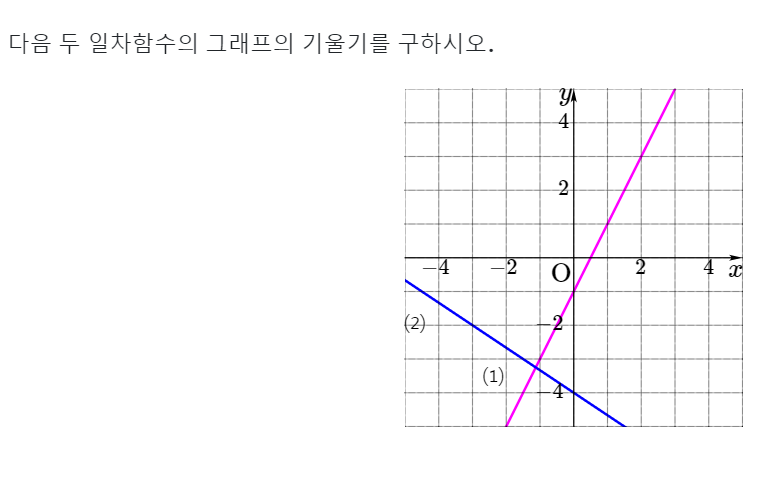
(1)번 직선을 보면 x의 값이 1 증가할 때, y의 값은 2 증가하므로 기울기가 2
(2)번 직선을 보면 x의 값이 3 증가할 때, y의 값은 2 감소하므로 기울기가 -3/2
이렇게 기울기의 개념을 설명했는데요, 아래는 더 많은 수학 문제를 연습할 수 있는 '모두매쓰'라는 곳에서 만든 문제입니다. 모두매쓰에서 충분히 연습해서 기울기에 대한 실전 감각을 길러보길 추천드립니다.
중등 2학년 수학 > 일차함수 > 기울기 개념, 일차함수 연습문제 프린트 학습지
'중등수학' 카테고리의 다른 글
| 중등 3학년 수학 > 이차함수 > 이차함수의 그래프의 평행이동 개념, 연습문제 프린트 학습지 (0) | 2024.07.05 |
|---|---|
| 중등 3학년 수학 > 이차함수 > 이차함수의 기본형 $ y=ax^2 $ 의 그래프 모양 연습문제 프린트 학습지 (0) | 2024.07.05 |
| 중등 2학년 수학 > 삼각형의 성질 > 삼각형의 내심과 외심 찾는 방법 연습문제 프린트 학습지 (0) | 2024.06.20 |
| 중등 2학년 수학 > 일차함수 > 일차함수의 그래프 그리기 연습문제 프린트 학습지 (0) | 2024.06.20 |
| 중등 1학년 수학 > 도형의 성질 > 정다각형의 한 내각 또는 한 외각 구하기 연습문제 프린트 학습지 (0) | 2024.06.20 |