중등 3학년 수학 > 이차함수 > 축의 방정식과 최댓값 또는 최솟값이 주어질 때, 미지수 a, b의 값 구하기 연습문제 프린트 학습지
축의 방정식
이차함수의 꼭짓점의 $x$좌표을 $a$라 하면 $x=a$가 축의 방정식입니다.
미지수가 포함된 이차함수식에서 축의 방정식과 최댓값 또는 최솟값이 주어질 때, 미지수의 값을 구하는 문제가 전형적으로 많이 나오는 문제유형입니다.
문제를 하나 풀어보겠습니다.

축의 방정식이 $x=3$이고, 최댓값이 $-4$이면, 이차함수의 꼭짓점의 좌표는 $(3,-4)$와 같습니다.
이차함수 $y=-x^2-3ax+b$를 꼭짓점을 구하는 식으로 변형하면,
$y=-(x^2+3ax)+b$
$y=-\left(x^2+3ax+\dfrac{9}{4}a^2-\dfrac{9}{4}a^2\right)+b$
$y=-\left(x+\dfrac{3}{2}a\right)^2+\dfrac{9}{4}a^2+b$
이때 이차함수의 꼭짓점의 좌표는 $\left(-\dfrac{3}{2}a,\dfrac{9}{4}a^2+b\right)$와 $(3,-4)$는 같은 값을 가지므로
$-\dfrac{3}{2}a=3$
$a=-2$
가 됩니다. 또한 $y$좌표를 비교하면,
$\dfrac{9}{4}a^2+b=-4$
$b=-13$
따라서 $ab=-2\times{(-13)}=26$입니다.
이렇게 축의 방정식과 최댓값 또는 최솟값이 주어질 때, 이차함수식의 미지수를 구하는 문제를 풀어봤습니다.
축의 방정식은 꼭짓점의 $x$좌표이고, $x$값의 구간이 정해지지 않은 이차함수의 경우, 최댓값 또는 최솟값이 꼭짓점의 $y$좌표와 같다는 것을 체크하시기 바랍니다.
아래는 위와 같은 유형의 문제를 프린트 할 수 있는 모두매쓰에서 만든 수학 문제입니다.
모두매쓰에서 같은 유형을 반복학습하시기를 추천드립니다.
그럼 좋은 하루되세요.
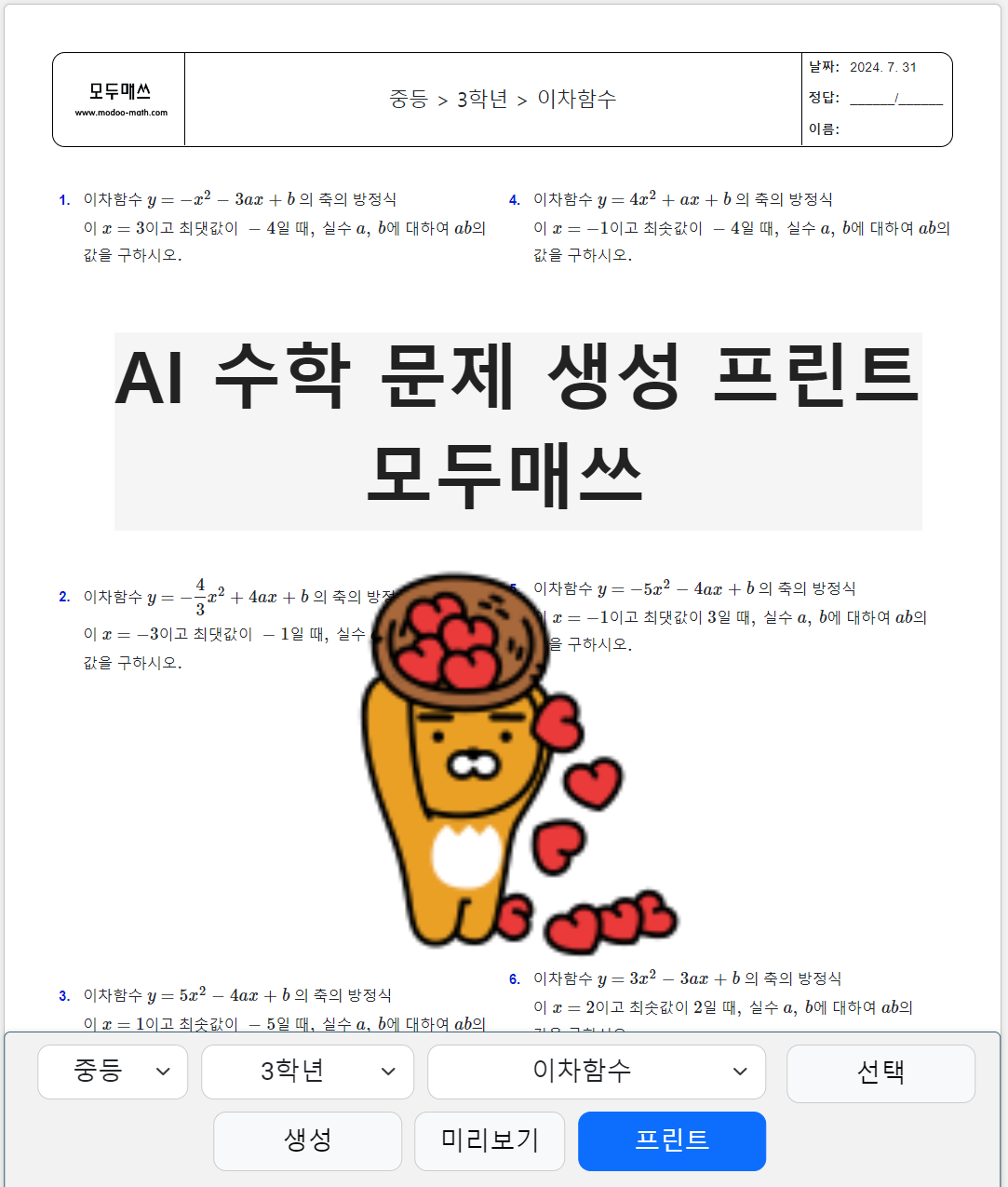
[모두매쓰 생성 문제]
중등 3학년 수학 > 이차함수 > 축의 방정식과 최댓값 또는 최솟값이 주어질 때, 미지수 a, b의 값 구하기 연습문제 프린트 학습지