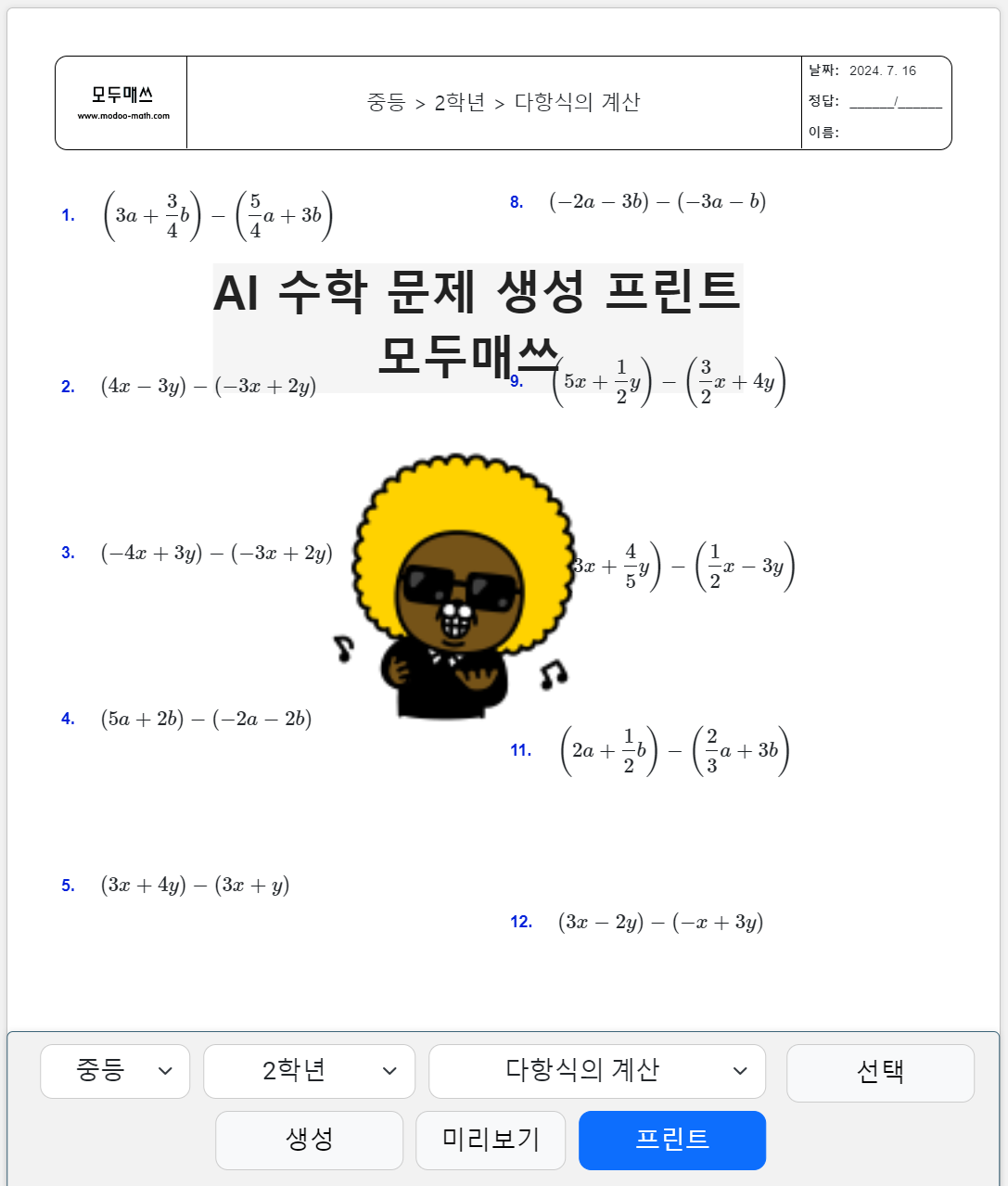
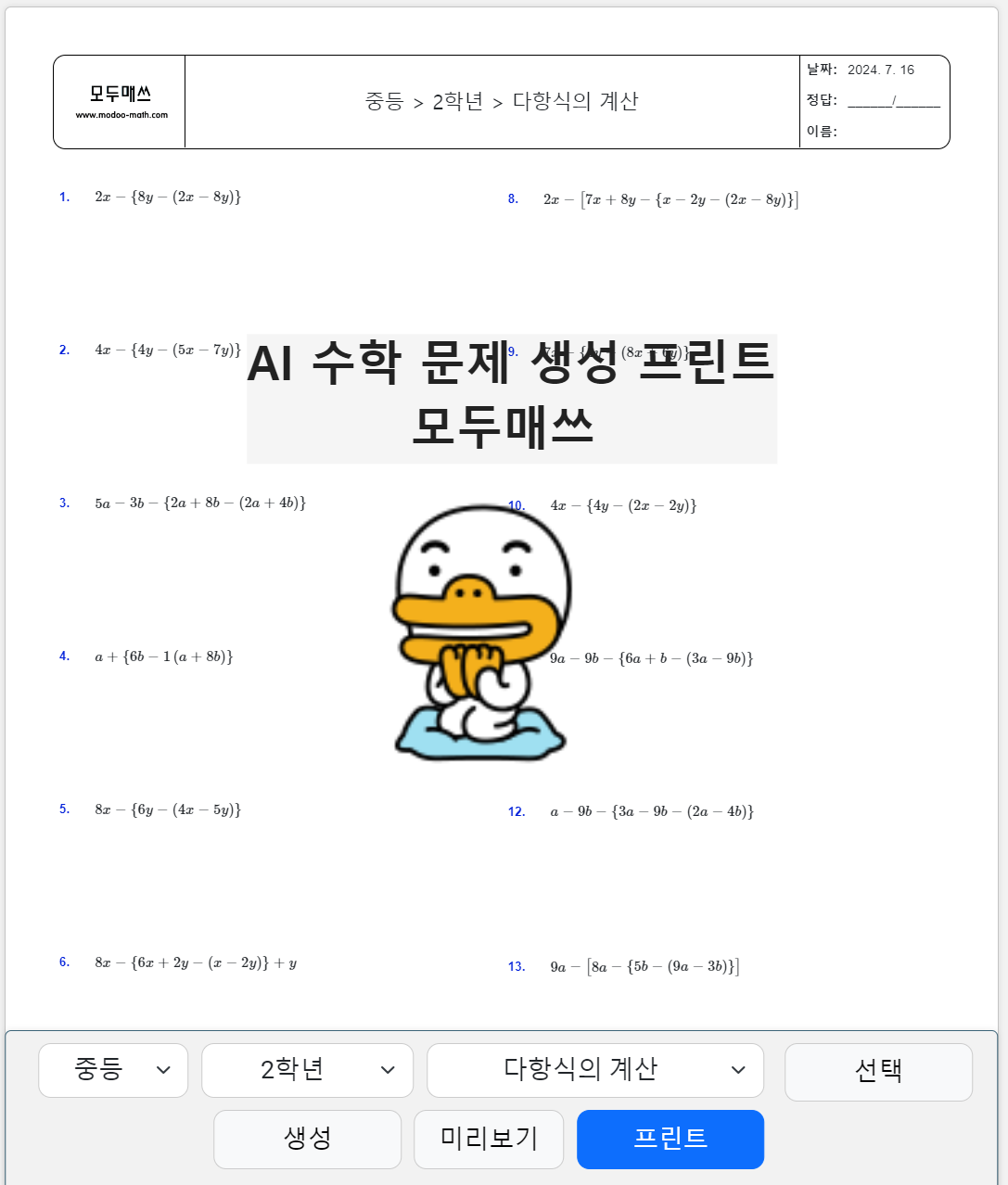
중등 2학년 수학 > 다항식의 계산 > 다항식의 덧셈과 뺄셈 연습문제 프린트 학습지

중등 2학년 수학 > 다항식의 계산 > 다항식의 덧셈과 뺄셈 연습문제 프린트 학습지

다항식의 개념

 

많은 학생들이 다항식의 개념에 대해 이렇게 대답을 합니다.

'항의 2개 이상인 식'

하지만 이건 엄밀하게 틀린 개념입니다. 

교과서를 펼쳐서 다시 보시면,

'항이 1개 또는 2개 이상인 식을 다항식이라고 한다'

라고 되어 있을거에요. 

'1개면 단항식 아닌가?' 

라고 생각할 수 있는데요, 맞아요. 단항식은 항이 1개인 식을 말해요. 

그런데 다항식이라고도 부를 수 있다는 것! 체크해보시길 바랍니다. 

 

그럼 다항식의 연산 중에서 덧셈과 뺄셈에 대한 연습문제를 함께 풀어보겠습니다. 

 

문제1)

우선 괄호를 풀어야 하는데요, 

괄호 앞에 $+$ 부호가 있으면 부호가 그대로 빠져나오고, 

괄호 앞에 $-$ 부호가 있으면 부호가 반대로 빠져나옵니다. 

$+$부호는 생략이 가능한데요, $(-5x-4y)$는 괄호 앞에 $+$부호가 생략되었다고 생각해야 합니다. 

 

$(-5x-4y)-(-5x+3y)$

$=-5x-4y+5x-3y$

$=-7y$

 

문제2)

괄호를 풀고 동류항끼리 계산을 합니다. 

$(2+3x-x^2)-(4x^2+3x+5)$

$=2+3x-x^2-4x^2-3x-5$

$=-5x^2-3$

 

문제3)

 

괄호의 계산 순서를 고려하여 정리하면, 

$2x-\{4x+3y-(3x-3y)\}-6y$

$=2x-(4x+3y-3x+3y)-6y$

$=2x-(x+6y)-6y$

$=2x-x-6y-6y$

$=x-12y$

 

 

문제4)

이번에는 분수형태로 된 문제입니다. 

분모를 통분하여 분자를 정리하면 됩니다. 

${\displaystyle \frac{a-b-1}{6}}-{\displaystyle \frac{a+b+1}{2}}+{\displaystyle \frac{a+b-1}{9}}$

 

$={\displaystyle \frac{3(a-b-1)}{18}}+{\displaystyle \frac{-9(a+b+1)}{18}}+{\displaystyle \frac{2(a+b-1)}{18}}$

 

$={\displaystyle \frac{3a-3b-3}{18}}+{\displaystyle \frac{-9a-9b-9}{18}}+{\displaystyle \frac{2a+2b-2}{18}}$

 

$={\displaystyle \frac{3a-3b-3-9a-9b-9+2a+2b-2}{18}}$

 

$={\displaystyle \frac{3a-9a+2a-3b-9b+2b-3-9-2}{18}}$

 

$={\displaystyle \frac{-4a-10b-14}{18}}={\displaystyle \frac{-2a-5b-7}{9}}$

 

$=-{\displaystyle \frac{2}{9}}a-{\displaystyle \frac{5}{9}}b-{\displaystyle \frac{7}{9}}$

 

 

문제5)

괄호가 포함된 식은 괄호 전체를 어떤 대문자로 표시해놓고 계산하면 편리해요. 

네모를 $A$라 하고 계산하면, 

 

$8a-[-7a+4b-\{5a-(A+2)\}]=17a-2b+3$

$8a-\{-7a+4b-(5a-A-2)\}=17a-2b+3$

$8a-(-7a+4b-5a+A+2)=17a-2b+3$

$8a-(-12a+4b+2+A)=17a-2b+3$

$8a+12a-4b-2-A=17a-2b+3$

$20a-4b-2-17a+2b-3=A$

$3a-2b-5=A$

정답은 1번입니다. 

 

이렇게 다항식의 연산 중에서 덧셈과 뺄셈에 대한 문제를 몇 개 풀어봤습니다. 

연습문제를 프린트해서 충분히 연습하고 싶으시면 '모두매쓰' 사이트를 이용하길 추천드립니다. 

수학 문제를 원하는 만큼 생성해서 프린트할 수 있어요. 

그럼 학습에 도움이 되셨길 바랍니다. 

 

 

 

 

 

중등 2학년 수학 > 다항식의 계산 > 다항식의 덧셈과 뺄셈 연습문제 프린트 학습지