
중1 수학 > 원과 부채꼴 > 부채꼴의 중심각, 호, 현, 넓이의 관계 (개념 + 연습문제 프린트 PDF)
부채꼴이란?

부채꼴은 쉽게 말해 원의 일부분이에요. 이때 아무렇게나 일부부은 아니고 원의 중심을 반드시 포함하고 있고 반지름과 호로 둘러싸여 있어야 해요.
부채꼴에 대한 용어를 살펴보면,
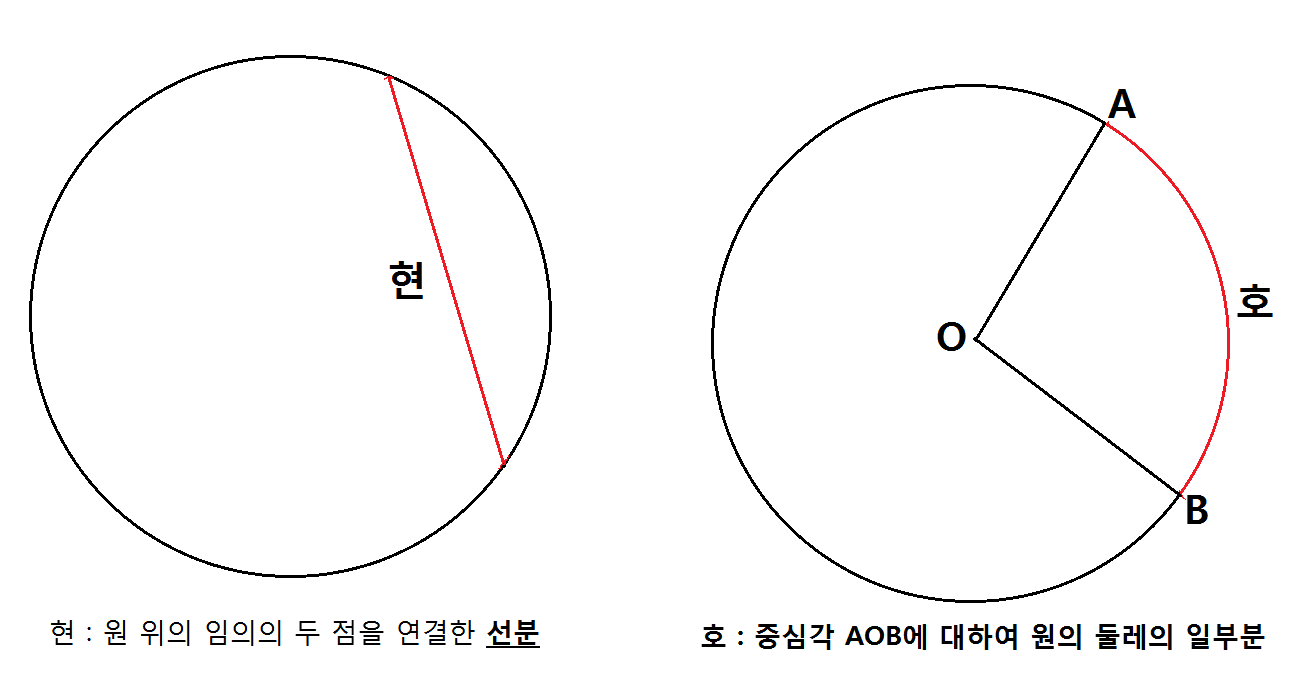


자 이렇게 기본적인 용어에 대해 살펴봤으니 본격적으로 부채꼴의 중심각, 호, 현, 부채꼴의 넓이의 관계에 대해 알아봐요.
부채꼴의 중심각, 호는 정비례 관계이다
정비례관계란 어느 하나가 2배, 3배, 4배, .. 씩 커질 때 똑같이 2배, 3배, 4배, .. 씩 커지는 관계를 말해요.
부채꼴의 중심각이 두 배가 되면 호의 길이도 두 배가 되는데요,
다음 그림을 참고하세요.

중심각의 크기가 2배이면 호의 길이도 2배가 된다
부채꼴의 중심각, 현은 정비례 관계가 아니다
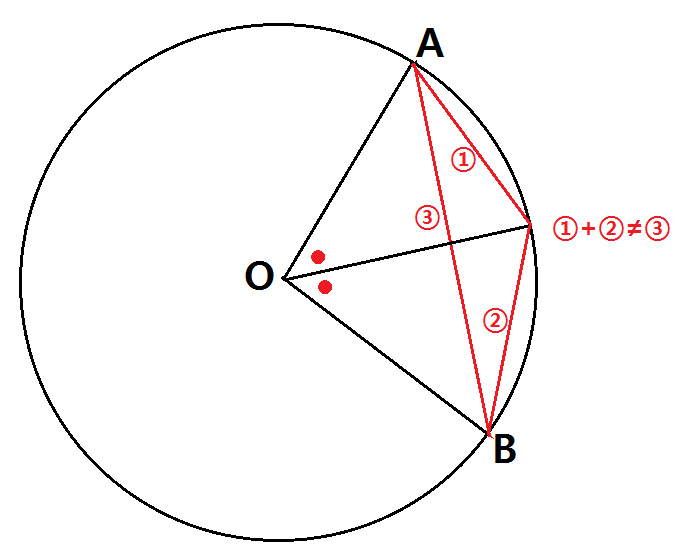
중심각의 크기는 2배이지만 현의 길이는 2배가 아니다
중심각이 2배가 될 때, 현은 2배가 되지 않아요. 따라서 정비례 관계는 아니에요.
부채꼴의 중심각, 부채꼴의 넓이는 정비례 관계이다

중심각의 크기가 2배가 되면 넓이도 정확히 2배가 되는 정비례 관계에요. 중심각이 3배면? 넓이도 3배가 되는거에요.

이제 이러한 개념을 가지고서 문제를 몇 개 풀어보도록 할게요.
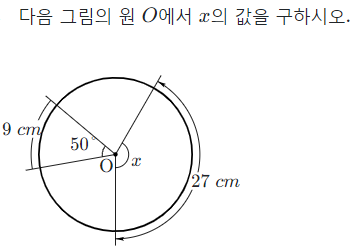
이 문제에서 중심각과 호의 관계를 알아야 해요. 방금 공부한 대로 호의 길이와 중심각의 크기는 정비례관계이므로 호의 길이가 3배이면 중심각의 크기도 3배이죠. 따라서 x=150˚ 입니다.

다음 문제는 부채꼴의 넓이와 중심각의 크기의 관계를 묻는 문제네요. 정비례 관계에 있으므로 중심각이 2배면 넓이도 2배가 되어야 해요. 따라서 넓이는 46 제곱센티미터가 되겠습니다.
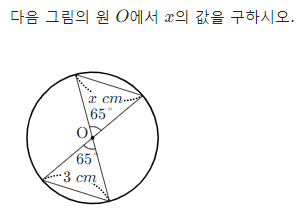
이 문제는 중심각의 크기와 현의 관계를 이용하는 문제예요. 여기서 주의해야할 것은 현과 중심각은 정비례관계는 아니지만 같은 중심각의 크기를 가지면 같은 현의 길이가 되는 건 맞아요.
따라서 x의 값은 3 cm입니다.
이렇게 부채꼴의 각 용어 개념과 부채꼴의 중심각, 현, 호, 넓이의 관계를 공부한 다음 몇 가지 문제를 풀어봤어요.
아래는 더 연습할 수 있는 문제를 PDF로 만들어 첨부한 거니 연습해보시길 바랍니다.
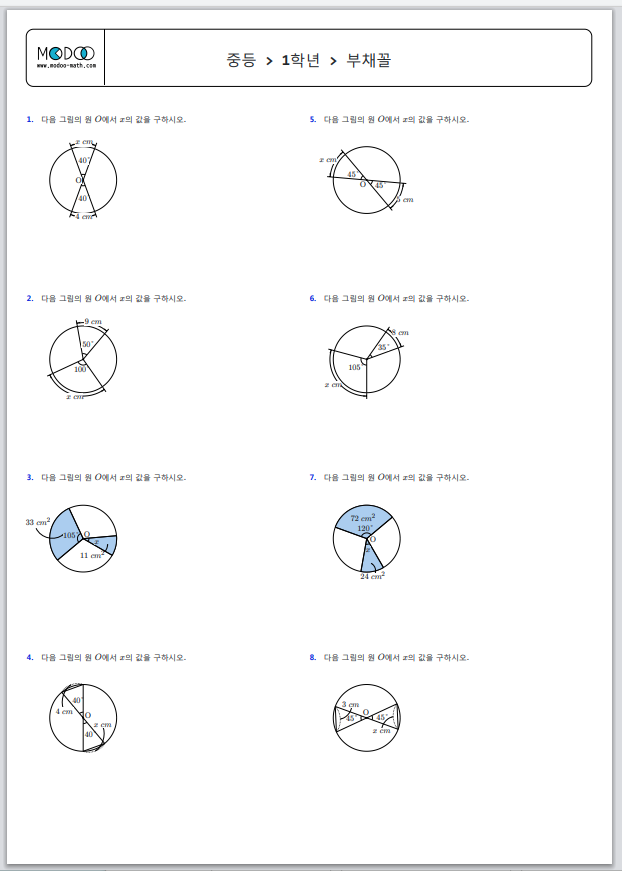
중1 수학 > 원과 부채꼴 > 중심각, 호, 현, 넓이의 관계 연습문제 프린트

'중등수학' 카테고리의 다른 글
| 중등 1학년 수학 > 도형의 성질 > 정다각형의 한 내각 또는 한 외각 구하기 연습문제 프린트 학습지 (0) | 2024.06.20 |
|---|---|
| 중등 1학년 수학 > 도형의 성질 > 다각형의 내각의 총합 구하는 공식과 원리, 연습문제 프린트 학습지 (0) | 2024.06.20 |
| 중등 1학년 수학 > 도형의 성질 > 다각형의 대각선의 개수 구하는 원리, 연습문제 프린트 학습지 (0) | 2024.06.20 |
| 중1 수학 > 기본도형 > 꼬인위치 개념, 연습문제 프린트 학습지 (0) | 2024.06.20 |
| 중등 1학년 수학 > 작도와 합동 > 삼각형의 결정조건(합동조건) 연습문제 프린트 학습지 (0) | 2024.06.20 |



