중등 3학년 수학 > 이차방정식 > 근의 공식 증명, 연습문제 프린트 학습지

 

모두매쓰 - 무제한으로 만들어지는 인공지능 수학 문제 생성 서비스

중등 3학년 수학 > 이차방정식 > 근의 공식 증명, 연습문제 프린트 학습지

 

이차방정식의 두 근을 구하는 공식은 다음과 같아요.

$$x=\dfrac{-b±\sqrt{b^2-4ac}}{2a}$$

근의 공식에 a, b, c의 값을 대입하여 계산하면 곧바로 해가 나오죠.

그런데 근의 공식을 굳이 유도과정을 알 필요가 있을까요? 그냥 공식에 대입하면 끝인데요.

왜냐하면 근의 공식에서 중요한 공식들이 많이 파생되기 때문이에요.

그럼 그 공식을 따로 암기하면 되지 않느냐구요? 네 물론 그렇게 해도 괜찮아요. 근데 공식을 잊어버릴 수 있지 않아요? 그럴때에는 공식의 유도과정과 파생되는 공식들을 알아두면 절대로 잊어버리지 않아요. 바로 암기 비법인셈이죠. 특히 근의 공식 유도과정은 다양한 식의 계산을 연습할 수 있는 좋은 재료이기도 해요. 또 다른 이유는 이차함수를 공부할 때 나오는 그래프와 관련된 공식들을 훨씬 더 이해를 잘할 수 있기 때문이기도 합니다.

​

그럼 근의 공식의 유도과정을 살펴볼게요.

이차항의 계수를 a로 이차항과 일차항을 동시에 묶어요.

$$ax^2+bx+c=0$$

$$a\left(x^2+\dfrac{b}{a}x\right)+c=0$$

다음으로 괄호안의 이차식을 완전제곱식으로 만들기 위해 ±(일차항의 계수 ÷ 2)제곱 으로 상수값을 가져와요.

$$a\left(x^2+\dfrac{b}{a}x+\dfrac{b^2}{4a^2}-\dfrac{b^2}{4a^2}\right)+c=0$$

이때, 이차항 + 일차항 + 상수 라는 3개의 항이 완전제곱식으로 만들 수 있는 세트가 되고 -상수는 필요없기에 괄호 밖으로 빼줘야 한답니다. 주의할 점은 이때 괄호 앞에 있는 a와 곱해서 밖으로 보내야 한다는 거에요.

두 가지를 같이 하면 헷갈릴 수 있으니, 완전제곱식에 필요없는 항을 먼저 a와 곱해서 괄호 밖으로 보낼게요.

$$a\left(x^2+\dfrac{b}{a}x+\dfrac{b^2}{4a^2}\right)+c-\dfrac{b^2}{4a}=0$$

 

이제 괄호 속의 식을 완전제곱시켜볼게요.

$$a\left(x+\dfrac{b}{2a}\right)^2+c-\dfrac{b^2}{4a}=0$$

 

이제 거의 다 왔어요. 조금만 더 힘을 내봐요. 근의 공식의 최종 목표는 바로 x의 값을 구하는 거에요. 그러니 한 쪽 변에 x만 남겨두고 나머지는 다른 쪽 변에 모두 넘겨줘야해요. 하나씩 짐들을 옮겨봐요.

한쪽 변에 제곱을 없애면 다른 쪽 변에 ±루트가 씌워져요.

이제 하나만 넘겨주면 돼요.

 

이게 바로 근의 공식이에요. 이걸로 문제를 풀어도 된답니다. 네? 뭔가 알던 공식과 다르다구요? 이게 더 복잡하다구요?

네 맞아요. 위의 식을 써도 되지만 좀 더 정리한다면 더 좋은 근의 공식이 될거에요. 조금 더 정리해볼까요?

우변을 보면 두 분수를 쉽게 통분할 수 있도록 되어 있어요.

 

이렇게 근의 공식을 유도하는 과정에 대해 살펴봤어요. 정말로 근의 공식을 쓰면 어떠한 이차방정식의 근도 모두 해결할 수 있을까요? 근의 공식을 적용하여 이차방정식의 문제를 풀어보도록 할게요.

​

이차방정식 하나를 가지고 왔어요. 근의 공식에 대입하려면 a, b, c의 값이 무엇인지 알아야 하겠죠. 위 식에서는

 

이므로 근의 공식에 대입하면,

 

근을 바로 구할 수 있다는 것을 확인할 수 있어요.

​

근의 공식을 암기하는 가장 좋은 방법은 이차방정식의 문제를 근의 공식을 적용해서 많이 풀어보는 거에요.

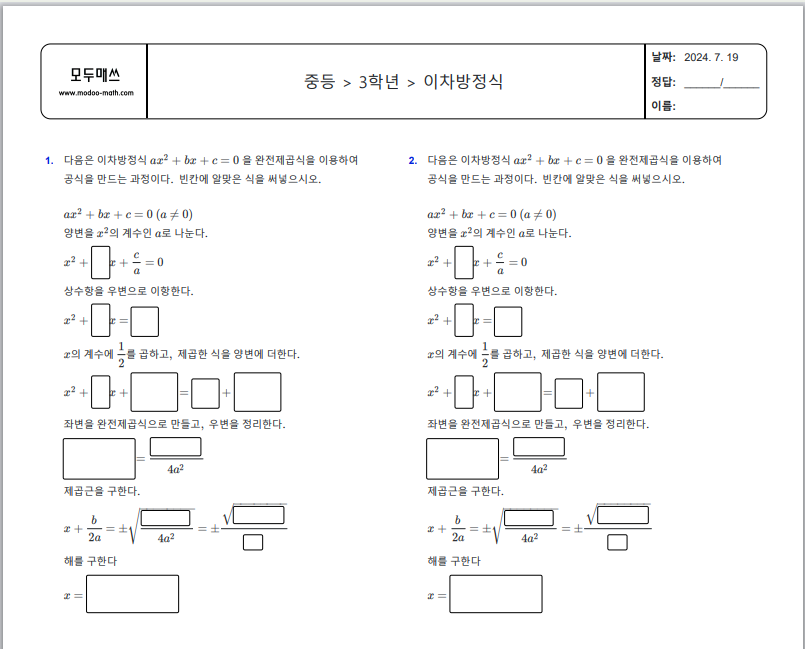
<모두매쓰에서 생성한 이차방정식 문제>

 

 

 

모두매쓰 - 무제한으로 만들어지는 인공지능 수학 문제 생성 서비스

중등 3학년 수학 > 이차방정식 > 근의 공식 증명, 연습문제 프린트 학습지