중등 1학년 수학 > 원과 부채꼴 > 부채꼴의 반지름의 길이 구하기 연습문제 프린트 학습지

 

모두매쓰 - 무제한으로 만들어지는 인공지능 수학 문제 생성 서비스

중등 1학년 수학 > 원과 부채꼴 > 부채꼴의 반지름의 길이 구하기 연습문제 프린트 학습지

부채꼴의 반지름 구하기: 개념과 문제풀이

부채꼴은 원의 일부를 차지하는 도형으로, 주어진 중심각과 호의 길이를 이용하여 반지름을 구할 수 있습니다. 이 글에서는 부채꼴의 반지름을 구하는 방법에 대해 설명하고, 예시 문제를 통해 이를 이해해보겠습니다.

1. 부채꼴의 개념

부채꼴은 원의 중심각과 원주 위의 두 점을 연결하는 호에 의해 형성된 도형입니다. 부채꼴의 중심각이 주어지고, 호의 길이가 알려져 있다면, 반지름을 계산할 수 있습니다.

2. 공식 설명

부채꼴에서 호의 길이 L은 다음 공식으로 구할 수 있습니다:

\[ L = 2\pi r \times \frac{\theta}{360} \]

여기서:

• L은 호의 길이
• θ는 중심각 (도 단위)
• r은 부채꼴의 반지름입니다.

3. 예시 문제풀이

문제:

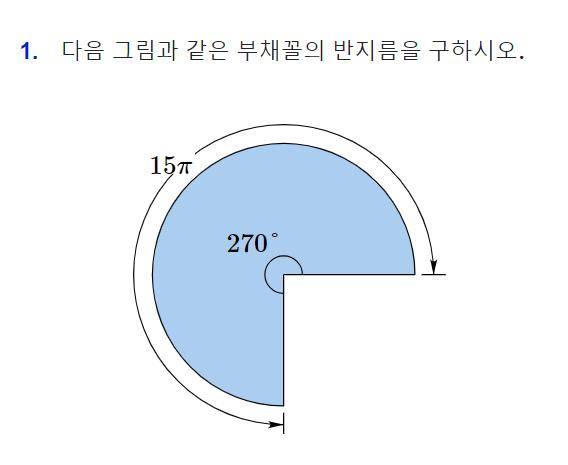
아래 그림과 같이 중심각이 270도이고 호의 길이가 15π인 부채꼴이 있습니다. 이 부채꼴의 반지름을 구하세요.

풀이:

먼저, 주어진 공식을 이용하여 반지름을 계산해보겠습니다. 호의 길이 L = 15π, 중심각 θ = 270°입니다. 이를 공식에 대입하면:

\[ 15\pi = 2\pi r \times \frac{270}{360} \]

양변을 단순화하면:

\[ 15\pi = 2\pi r \times \frac{3}{4} \]

양변을 \(\pi\)로 나누고 정리하면:

\[ 15 = r \times \frac{3}{2} \]

양변에 2를 곱하고, 3으로 나누면:

\[ r = 10 \]

따라서, 이 부채꼴의 반지름은 10입니다.

4. 모두매쓰(Moodo Math) 추천

이처럼 다양한 수학 문제를 해결하기 위해, 모두매쓰와 같은 도구를 사용하는 것도 좋은 방법입니다. 모두매쓰는 인공지능을 활용하여 초등, 중등, 고등 수학 문제를 무제한으로 생성해주는 서비스로, 학생들이 필요한 문제를 쉽게 찾아 풀 수 있도록 도와줍니다. 문제를 프린트하거나 화면에서 바로 풀 수 있으며, 각 문제의 유형과 난이도를 개인 맞춤형으로 설정할 수 있습니다.

모두매쓰를 통해 꾸준히 수학을 연습하면서 다양한 유형의 문제를 접하고, 실력을 향상시켜보세요.

 

 

모두매쓰 - 무제한으로 만들어지는 인공지능 수학 문제 생성 서비스